Unconstrained Cyclist Trajectory Simulation for agent-based models

Abstract

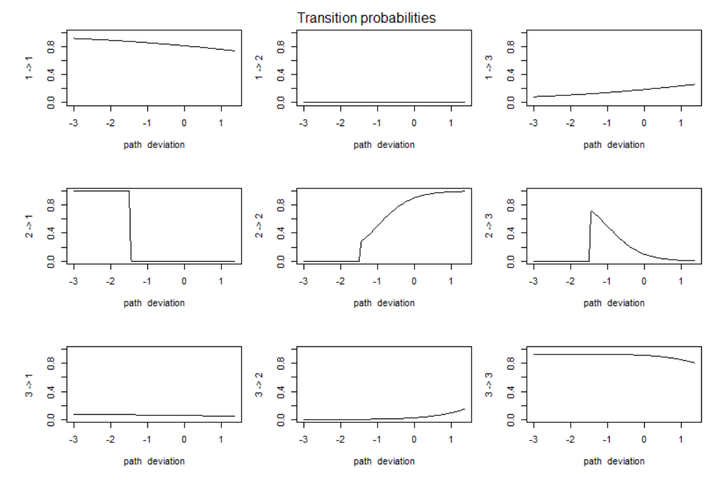
Bicycle microsimulation models can have many uses including bicycle facility assessment, bicycle energy and power modeling and bicycle behavior prediction models for safety applications. Agent-based modeling (ABM) is a promising approach for building accurate bicycle microsimulation models.An agent-based model represents individual agents interacting on the microscopic level by assuming sensory inputs give the agents information about the environmentwhich informs their decisions (Plekhanova, 2003). The environment of bicycle traffic on cycling paths includes bicycle facility geometry (bicycle path lane width, curves, grades,…), and other cyclists that can differ in their proximity (longitudinal or lateral). Previous research has shown that cyclists encounter different regimes of movement during their trips(Mohammed, Bigazzi, & Sayed, 2019). Cyclists can be in a constrained regime (their actions are correlated/dependent on the movement of other cyclists), or in an unconstrained regime (their actions are not affected by other cyclists). Previous research in bicycle microsimulation includes attempts to model bicycle traffic in a cellular automata model (Jiang, Jia, & Wu, 2004; Xue, Jia, Jiang, Li, & Shan, 2017). Liang et al. (2012) developed a psychological-physical force model that assumes cyclists choose their trajectories (acceleration and direction) based on forces of collision avoidance and friction between interacting cyclists. Mohammed et al. (2019) developed a bicycle following model based on learning the reward function of cyclists using inverse reinforcement learning. No previous research exists for modeling unconstrained cyclist trajectories. Although unconstrained cyclists may seem to move arbitrarily, it is hypothesized that their movements can be modeled given variables such as acceleration, change in direction and deviation from path centerline. Unconstrained cyclist trajectories can be thought of as correlated random walk movements, in which the state of the present time step is dependent on the previous time step. Hidden Markov Models (HMM) can be used to infer the hidden states that cyclist encounter at each time step given observations about their movement. The purpose of this research is to formalize a generative model that can describe unconstrained cyclist movement and be used to generate cyclist trajectories that are similar to observed ones. This model can then be combined with other constrained bicycle models to generate realistic interactions for bicycle microsimulation.